

Evaluate the lsolve function using the matrix and the vector as the inputs.Create a vector of the constants appearing on the right-hand side of the system of equations.Create a matrix that contains the coefficients of the variables in your system of equations.To use lsolve, perform the following steps: Mathcad has a built-in function for solving a linear system of equations called lsolve. In a nonlinear system, one or more variables are raised to a power higher than one.Īlso, Mathcad will warn you if you have an inconsistent system of equations-that is, one for which a solution does not exist.
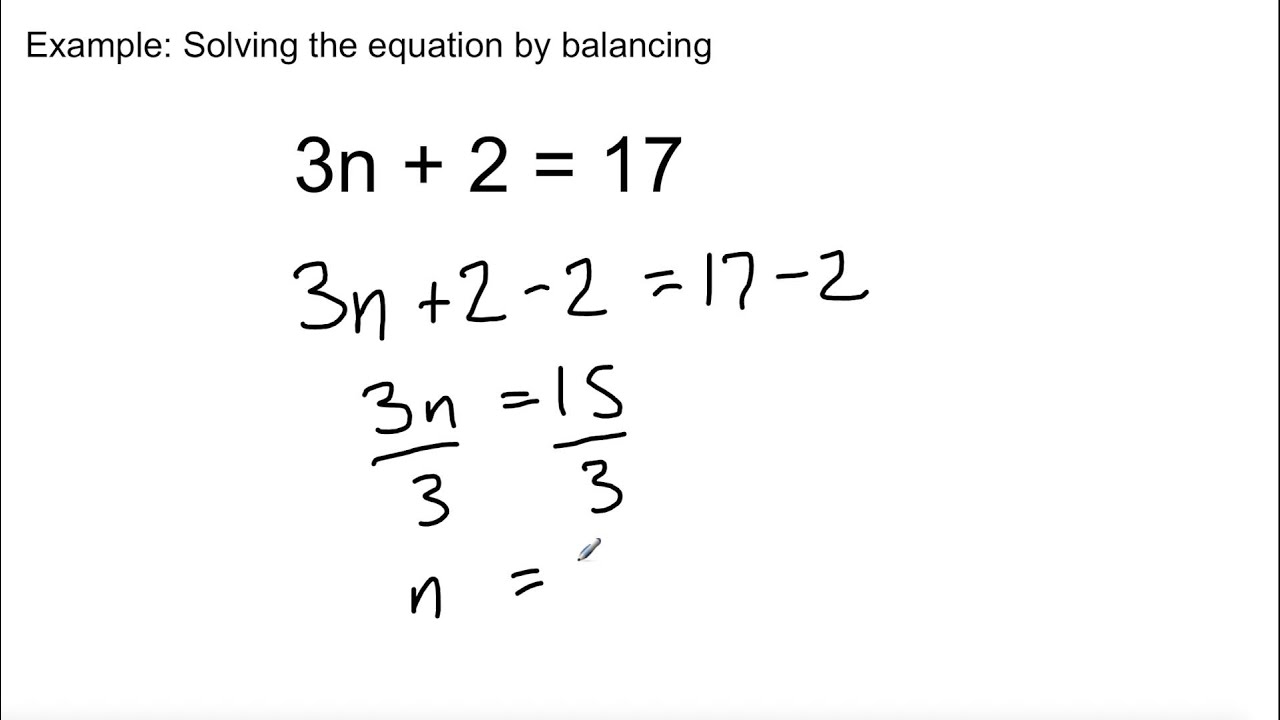
A linear system is one in which the variables are all raised to the first power and the equation results in a line. I like Solve Blocks because they can be used to solve both linear and nonlinear systems of equations. Then outside of the Solve Block, evaluate the vector or individual variables to see the solutions. Then use the Definition operator to assign the Find function for the same variables. Solver: create a vector for the variables you want to solve for.

Note that you use the Comparison operator, not the Evaluation operator, for the equals sign. Constraints: you write your system of equations here.If I have no idea what to use, I will use a value of 1. Guess Values: in this section, you initialize the variables that you want to solve for using the Definition operator to assign a value.The Solve Block is initiated from the Math tab.
#SOLVE EQUATION SYSTEMS HOW TO#
If you are going to use Mathcad for engineering calculations, I highly recommend you learn how to use this construct. In addition to solving systems of equations, it can be used to perform optimizations – finding the minimum or maximum for a function – and differential equations. The Solve Block is a special structure in Mathcad. Let’s take a look at how to use each of these methods. PTC Mathcad has a few methods that we can use to solve for the variables. Real-world examples that require solving a system of equations include Kirchhoff’s Law for electrical resistance and aerodynamic trajectories.
#SOLVE EQUATION SYSTEMS SERIES#
They are called dependent systems and their solutions are expressed using the notation ( x, m x + b ), where x is any real number.In math and engineering, we often are left with a series of equations with an equal number of variables that we want to solve for. These systems consist of equations that are equivalent and represent the same line. Some linear systems have infinitely many simultaneous solutions.They are called inconsistent systems and the solution set is the empty set, Ø. These systems consist of equations that represent parallel lines with different y-intercepts and do not intersect in the plane. Some linear systems have no simultaneous solution.It is a good practice to always check your solutions. The graphing method is not the most accurate method for determining solutions, particularly when a solution has coordinates that are not integers.The graphing method for solving linear systems requires us to graph both of the lines on the same set of axes as a means to determine where they intersect.Geometrically, solutions are the points where the graphs intersect. Solutions to such systems, if they exist, consist of ordered pairs that satisfy both equations. In this section, we limit our study to systems of two linear equations with two variables.To check that an ordered pair is a solution, substitute the corresponding x- and y-values into each equation and then simplify to see if you obtain a true statement for both equations. In this case, (3, 2) is the only solution. For example,Ī solution to a linear system Given a linear system with two equations and two variables, a solution is an ordered pair that satisfies both equations and corresponds to a point of intersection., or simultaneous solution Used when referring to a solution of a system of equations., is an ordered pair ( x, y) that solves both of the equations. consisting of two linear equations each with two variables. In this section, we will study linear systems A set of two or more linear equations with the same variables. consists of a set of two or more equations with the same variables.

A system of equations A set of two or more equations with the same variables. Real-world applications are often modeled using more than one variable and more than one equation. Definition of a Linear System with Two Variables


 0 kommentar(er)
0 kommentar(er)
